- Fortran95
- MPI
- OpenMP
Key words
- electronic transport
- electron-phonon interaction
- Born approximation
- Lowest Order Expansion
- non-equilibrium Green's function
- density functional theory
Introduction
The quantum electronic transport code SMEAGOL (Spin and Molecular Electronics Algorithm on a Generalized atomic Orbital Landscape) [1, 2] is based on the non-equilibrium Green’s function (NEGF) formalism for one-particle Hamiltonian. In its present form it uses density functional theory (DFT) with the numerical implementation contained in the code SIESTA [3, 4]. However, SMEAGOL’s computational scheme is very general and can be implemented together with any electronic structure methods based on localized basis sets. Alternative implementations are currently under investigation.
This version of the code, called Inelastic SMEAGOL, has a number of improvements, bug fixes and new implementations. The first major change was the transitioning from the deprecated version 1.3 of SIESTA code to the new version 3.1. The new implementations include the possibility of performing molecular dynamics together with transport calculations, a more efficient calculation of the self-energies from periodic leads and the electronic transport with electron-phonon interaction in the Born approximation [5].
For a comprehensive user guide of the of the standard functionalities of the code refer to SMEAGOL User’s Guide [6]. Here it will be discussed only the new implementations.
Periodic Leads
In case of leads, which are periodic in all directions, the resources needed for computing the electrodes’ self-energies in the non-equilibrium transport calculation can be reduced if one considers their periodicity in the direction perpendicular to transport.
For that purpose one needs to perform another lead calculation but considering only the lead’s unit cell and with a different SystemLabel, say SystemLabelSmall.
Input flags
In addition the input flags for bulk calculation (see SMEAGOL User’s Guide [6]), the following input flags must be supplied to the input.fdf file in order to perform the periodic lead calculation.
PeriodicLead (Boolean): When this flag is set to true the information about the positions of atomic orbitals for mounting the corresponding lead supercell is written to the file
SystemLabelSmall.xij.Default value:
F
InitTransport (Boolean): When this flag is set to true the supercell size is expanded to 3 in transverse directions.
Default value:
F
Output files
Similarly to the bulk calculation (see SMEAGOL User’s Guide [6]) the files bulklft.DAT and bulkrgt.DAT are generated.
But since they have the same name, one should rename these files as bulklftsmall.DAT and bulkrgtsmall.DAT, respectively.
In addition, the following file is generated:
SystemLabelSmall.HSL: File containing the Hamiltonian and overlap matrices of the leads. The string
SystemLabelSmallis read from eitherbulklftsmall.DATorbulkrgtsmall.DAT. If the two leads are the same one can use the sameSystemLabelSmall.HSLfile to read the information for both the left and right leads (set the flagBulkLeadstoLR). If the two systems are different, then two files with different names must be provided from two different leads calculations (set the flagBulkLeadsto eitherLorR).
SystemLabelSmall.xij: File containing the positions of atomic orbitals which are used for mounting the corresponding lead supercell in transport calculations.
Example
In order to understand the periodic lead procedure, let’s consider the example of a gold electrode, which has a face-centered cubic crystal structure, with a supercell consisting of 27 atoms (three layers of 9 atoms) as represented in Figure 1 below. We note that this supercell can be reproduced by repeating the highlighted atoms 3 times in either x and y directions.
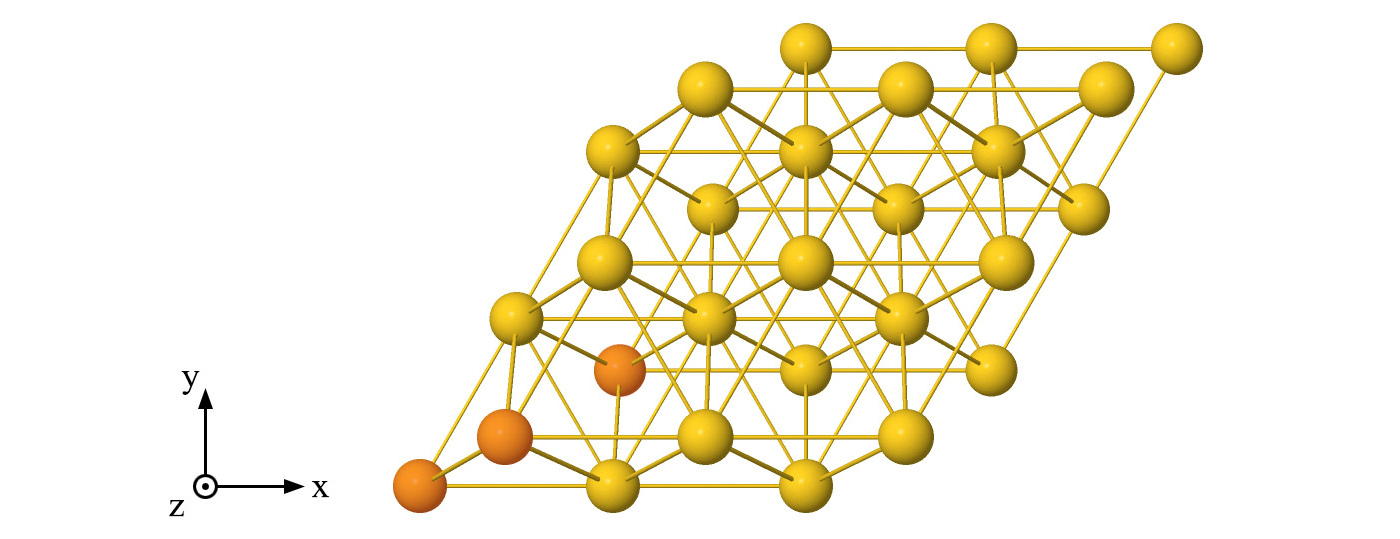
Figure 1: Example of solid lead supercell constituted by 27 gold atoms which are repeated periodically in all directions. The lead’s unit cell containing 3 gold atoms is highlighted.
At the usual leads calculation, one should have the following parameters at the input.fdf file (refer to the SIESTA manual for a detailed description of the input flags):
LatticeConstant 1.0 Bohr
%block LatticeVectors
16.775105494 0.000000000 0.000000000
8.387552747 14.527653318 0.000000000
0.000000000 0.000000000 13.696815999
%endblock LatticeVectors
%block kgrid_Monkhorst_Pack
1 0 0 0.0
0 1 0 0.0
0 0 100 0.0
%endblock kgrid_Monkhorst_Pack
AtomicCoordinatesFormat NotScaledCartesianBohr
AtomCoorFormatOut NotScaledCartesianBohr
%block AtomicCoordinatesAndAtomicSpecies
9.371155587 7.007825359 0.000000000 1 1 Au
3.779453756 3.779453756 4.565599034 1 2 Au
6.575304671 5.393639557 9.131216965 1 3 Au
14.962857418 7.007825359 0.000000000 1 4 Au
9.371155587 3.779453756 4.565599034 1 5 Au
12.167006503 5.393639557 9.131216965 1 6 Au
20.554559250 7.007825359 0.000000000 1 7 Au
14.962857418 3.779453756 4.565599034 1 8 Au
17.758708334 5.393639557 9.131216965 1 9 Au
12.167006503 11.850382764 0.000000000 1 10 Au
6.575304671 8.622011161 4.565599034 1 11 Au
9.371155587 10.236196962 9.131216965 1 12 Au
17.758708334 11.850382764 0.000000000 1 13 Au
12.167006503 8.622011161 4.565599034 1 14 Au
14.962857418 10.236196962 9.131216965 1 15 Au
23.350410165 11.850382764 0.000000000 1 16 Au
17.758708334 8.622011161 4.565599034 1 17 Au
20.554559250 10.236196962 9.131216965 1 18 Au
14.962857418 16.692940169 0.000000000 1 19 Au
9.371155587 13.464568566 4.565599034 1 20 Au
12.167006503 15.078754368 9.131216965 1 21 Au
20.554559250 16.692940169 0.000000000 1 22 Au
14.962857418 13.464568566 4.565599034 1 23 Au
17.758708334 15.078754368 9.131216965 1 24 Au
26.146261081 16.692940169 0.000000000 1 25 Au
20.554559250 13.464568566 4.565599034 1 26 Au
23.350410165 15.078754368 9.131216965 1 27 Au
%endblock AtomicCoordinatesAndAtomicSpecies
In this example, the lead’s unit cell calculation is performed considering only three gold atoms (those highlighted in Figure 1) and the k-points in x and y directions should be multiplied by 3 as follows:
LatticeConstant 1.0 Bohr
%block LatticeVectors
5.591701831 0.000000000 0.000000000
2.795850916 4.842551106 0.000000000
0.000000000 0.000000000 13.696815999
%endblock LatticeVectors
%block kgrid_Monkhorst_Pack
3 0 0 0.0
0 3 0 0.0
0 0 100 0.0
%endblock kgrid_Monkhorst_Pack
AtomicCoordinatesFormat NotScaledCartesianBohr
AtomCoorFormatOut NotScaledCartesianBohr
%block AtomicCoordinatesAndAtomicSpecies
9.371155587 7.007825359 0.000000000 1 1 Au
3.779453756 3.779453756 4.565599034 1 2 Au
6.575304671 5.393639557 9.131216965 1 3 Au
%endblock AtomicCoordinatesAndAtomicSpecies
Here, it is important to note that the order within the AtomicCoordinatesAndAtomicSpecies block in the calculations for the large leads should be taken into consideration.
It should be built by repeating the small electrodes n1 times in the direction of the first lattice vector, and n2 times in the direction of the second lattice vector.
It is also important to note that the kgrid_Monkhorst_Pack block for the small leads calculation should be given by
%block kgrid_Monkhorst_Pack
n1 x nk1large 0 0
0 n2 x nk2large 0
0 0 nk3large
%endblock kgrid_Monkhorst_Pack
if we define the kgrid_Monkhorst_Pack for the large electrode as
%block kgrid_Monkhorst_Pack
nk1large 0 0
0 nk2large 0
0 0 nk3large
%endblock kgrid_Monkhorst_Pack
I-V calculation
Once the initial calculation for the leads has been performed we can proceed with computing the non-equilibrium transport properties of our system.
Input files
Several files generated during the construction of the leads must be used. These are: bulklft.DAT, bulkrgt.DAT, SystemLabel.HSL and SystemLabel.DM.
In case of periodic leads one should include also the files bulklftsmall.DAT, bulkrgtsmall.DAT, SystemLabelSmall.HSL and SystemLabelSmall.xij.
Flags specific of calculations involving periodic leads
PeriodicLead (Boolean): If true I-SMEAGOL will perform a periodic leads calculation. This requires files
SystemLabelSmall.HSL,SystemLabelSmall.xij,bulklftsmall.DATandbulkrgtsmall.DATshould be present.Default value:
F
LatticeConstantLeads (Physical): Lattice constant parameter used at the lead unit cell calculation.
Default value: 1.0 Bohr
LeadsLatticeVectors (data block): Contains the 3 lattice vectors of the unit cell of the small electrodes.
Default value: No Default
LeadsSuperCell (data block): The number of repetitions for the first and cell leads lattice vectors. The values in the block should be integer numbers.
Default value: No Default
It is important to note that each cell vector multiplied by the corresponding LeadsSuperCell factor should be equal to the LatticeVector defined in the input.fdf file.
Example for periodic lead calculation
Considering the example used to setup the electrodes in Example above, in the input.fdf file, one should use the following flags:
LatticeConstantLeads 1.0 Bohr
%block LeadsLatticeVectors
5.591701831 0.000000000 0.000000000
2.795850916 4.842551106 0.000000000
0.000000000 0.000000000 13.696815999
%endblock LeadsLatticeVectors
%block LeadsSuperCell
3 3
%endblock LeadsSuperCell
We note that the LeadsLatticeVectors correspond to the lattice vectors used for the small electrodes calculations, and the LeadsSuperCell is given by:
%block LeadsSuperCell
n_1 n_2
%endblock LeadsSuperCell
Inelastic I-V calculation
In the I-SMEAGOL code, weak electron-phonon interactions can be considered by the so-called first Born approximation (1BA) and self-consistent Born approximation (SCBA) [5]. Their interaction self-energies are represented in diagrammatic form in Figure 2.
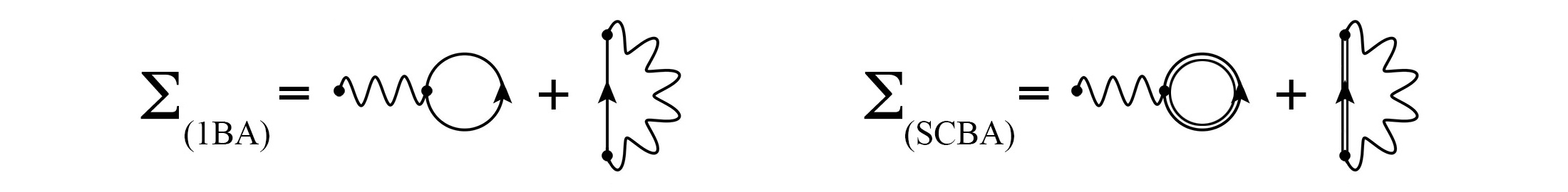
Figure 2: Diagrammatic representation of the first Born approximation (left) and the self-consistent Born approximation (right).
In the first Born approximation one considers only the first order terms of the electronic Green’s function expansion. The two first order diagrams can be identified, from left to right, as the Hartree and the Fock diagrams. In the self-consistent Born approximation, the interaction self-energy is calculated with the perturbed electronic Green’s function in a self-consistent way.
Input files
In addition to the files required for usual I-V calculation (see above), another file containing the vibrational analysis (electron-phonon couplings and vibrational frequencies) must be supplied:
FileEPh: The first line contains integer numbers separated by white spaces corresponding to the following information: the number of spin components, the number of dynamic atoms (those that were displaced on force constant calculation for the vibrational analysis), the number of dynamic orbitals, the first dynamic orbital index and the last dynamic orbital index. The next line contains the vibrational frequencies (in eV) separated by white spaces (if it was considered n atoms in the vibrational analysis, then there should have 3n frequencies). The following lines contains the electron-phonon coupling matrices (in eV) in the same order as the frequencies (for each frequency there must have one electron-phonon coupling matrix).
Input flags
In addition to the input flags required for usual I-V calculation (see SMEAGOL User’s Guide [6]), the following input flags must be supplied to the file input.fdf in order to perform inelastic transport (I-V) calculations.
Inelastic (Boolean): If true I-SMEAGOL will perform NEGF transport calculation with inelastic scattering given by the first Born approximation or/and the self-consistent Born approximation. Otherwise, the code will perform the usual elastic transport calculation.
Default value:
F
ElectronPhononMatrix (String): Name of the file containing the electron-phonon coupling matrices and the vibrational mode frequencies.
Default value: No Default
SCBA (Boolean): If true the code will compute the self-consistent Born approximation. If false I-SMEAGOL will calculate only the first Born approximation.
Default value:
F
SCBAconv (Double precision): Self-consistent convergence criteria. The self-consistency is achieved when the difference | ∑nSCBA - ∑n-1SCBA |, between the new self-energy and the one calculated on the last cycle, is lower than
SCBAconv.Default value: 10-4
SCBAmix (Double precision): It is a real number in [0, 1] which defines the self-energies mixing factor for the self-consistent procedure. At each cycle, the previous self-energy is redefined as ∑nSCBA = (1-SCBAmix) ∗ ∑n-1SCBA + SCBAmix ∗ ∑nSCBA. A lower value for SCBAmix is better to ensure the convergence, but also reduces the rate of convergence.
Default value: 10-1
MaxSCBAIterations (Integer): Maximum number of self-consistent iterations. If the self-consistency was not achieved after
MaxSCBAIterationscycles, the code will stop the self-consistent procedure and will consider the self-energy from the last cycle as a converged one.Default value: 500
Hartree2 (Boolean): If true the code will use calculated density matrix to compute the Hartree diagram contribution. Otherwise it computes the Hartree term independently.
Default value:
F
NEnergInel (Integer): Number or energy points along the real axis used for computing some integrals at inelastic transport (the current and the non-equilibrium part of the Hartree diagram). If
SCBAis false (i.e. only the first Born approximation is considered) the points are distributed between -(V/2 + 30kBT + 2Ωmax) and (V/2 + 30kBT + 2Ωmax), where Ωmax is the highest vibrational frequency. IfSCBAis true the points are distributed between -(EB + 2Ωmax) and (V/2 + 30kBT + 2Ωmax), where EB is theEnergLowestBound(see SMEAGOL User’s Guide [6]). In the last case a much large number of points is needed.Default value: 1000
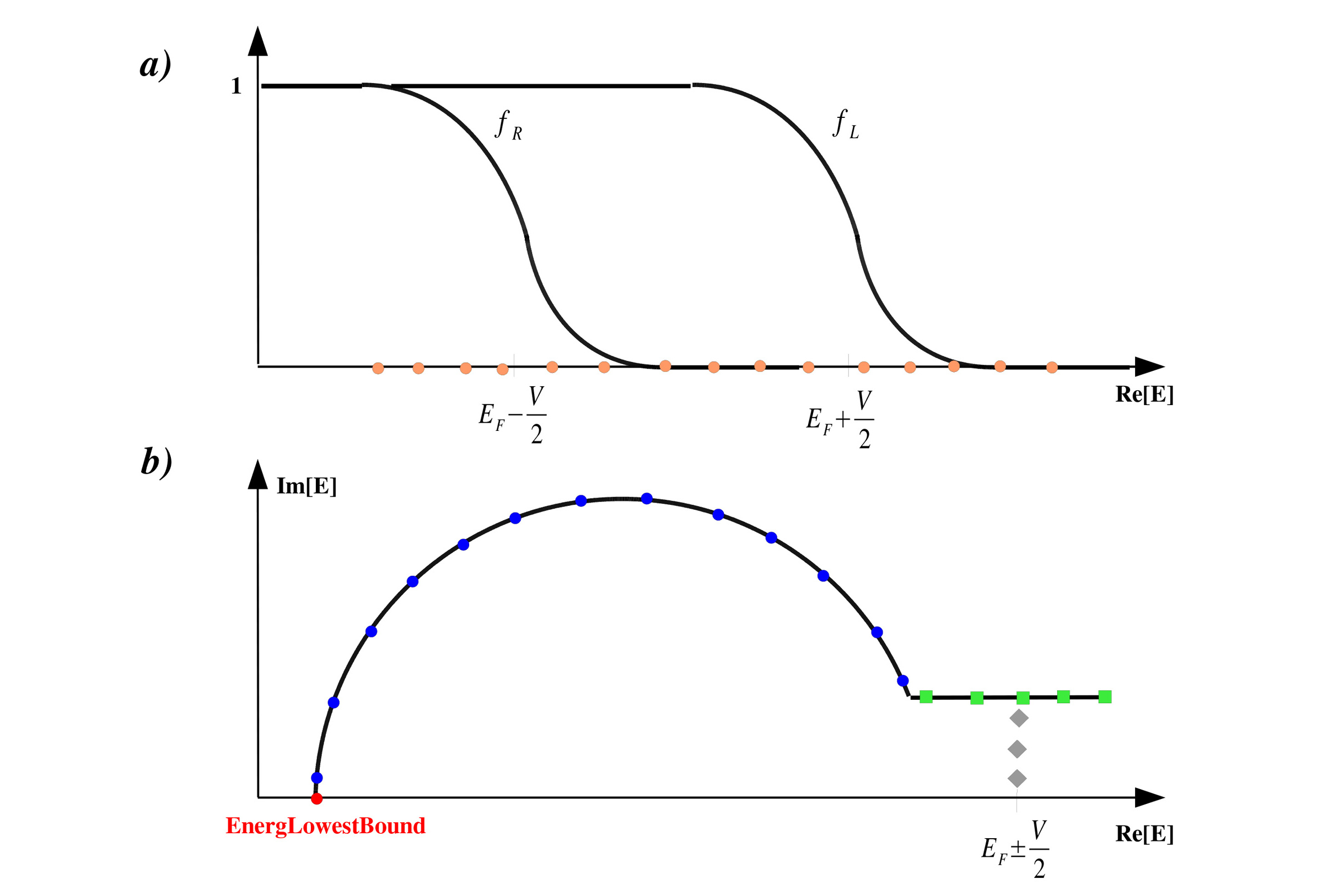
Figure 3:
Sketches for the Green Function integration leading to the non-equilibrium charge density [1, 2].
(a) The non-equilibrium part must be performed along the real energy axis, but is bound by the left- and right-hand side Fermi distributions functions, fL and fR.
(b) The equilibrium component is performed over a semicircular path in the complex energy plane.
Here we show the starting position EnergLowestBound, the energy mesh along the two segments of the curve and the poles of the Fermi distribution.
iNEnergImCircle (Integer): As in elastic transport, where the equilibrium part of the Green’s function integral is calculated in a contour in the complex plane, in inelastic transport one need to perform the same kind of integrals for computing the equilibrium part of the Hartree diagram and for computing some terms of the Fock diagram. Therefore, the flag
iNEnergImCircleindicates the number of energy points along the semi-circle in the complex plane (see Figure 3 (b) for a sketch of the points along the contour in the complex energy plane, where the points on the semi-circle are represented by blue points).Default value: 34
iNEnergImLine (Integer): Number of energy points along the line in the complex plane contour used for computing integrals (see Figure 3 (b) for a sketch of the points along the contour in the complex energy plane, where the points on the line part are represented by green points).
Default value: 20
iNPoles (Integer): Number of poles in the Fermi distribution used for computing integrals on the complex plane. It specifies how far from the real axis the contour integral will be performed (see Figure 3 (b) for a sketch of the points along the contour in the complex energy plane, where the poles inside the contour are represented by gray diamonds).
Default value: 5
fullDOS (Boolean): If true the code will compute the total density of states (DOS) with the interacting Green’s function. Regardless of this option the code calculates the local density of states of the dynamic atoms.
Default value:
F
Output files
The following files contain the I-V characteristics:
SystemLabel.I0CUR: File containing the elastic I-V characteristics.
SystemLabel.I1BA0CUR: File containing the “elastic” I-V characteristics of the first Born approximation (i.e. the elastic current computed with the interacting 1BA Green’s function).
SystemLabel.I1BACUR: File containing the total (elastic and inelastic) I-V characteristics of the first Born approximation.
SystemLabel.ISCBA0CUR: File containing the “elastic” I-V characteristics of the self-consistent Born approximation (i.e. the elastic current computed with the interacting SCBA Green’s function).
SystemLabel.ISCBACUR: File containing the total (elastic and inelastic) I-V characteristics of the self-consistent Born approximation.
In case of spin polarized calculation the *CUR files above contain four columns, where the first corresponds to the bias in eV, the second column corresponds to the total current and the third and fourth columns (in the case of a spin-dependent calculation) correspond to the spin-decomposed current.
In case of non-polarized spin calculation these files contain only the first two columns.
The following files contain the local density of states (LDOS) of dynamic atoms computed at bias IV:
SystemLabel_IV.IA0: Local density of states of dynamic atoms computed at bias
IVwith non-interacting Green’s functions.
SystemLabel_IV.IA1BA: Local density of states of dynamic atoms computed at bias
IVwith 1BA Green’s functions.
SystemLabel_IV.IASCBA: Local density of states of dynamic atoms computed at bias
IVwith SCBA Green’s functions.
In case of spin polarized calculation the *IV.IA* files contain three columns, where the first corresponds to the energy (subtracted by the Fermi energy) and the second and third columns corresponds to the LDOS for up and down spins, respectively.
In case of non-polarized spin calculation these files contain only a second column containing the LDOS.
If fullDOS is set to T, the following files contain the total density of states (DOS) computed at bias IV:
SystemLabel_IVf.IA0: If
fullDOSis set toT, this file contains the total density of states computed at biasIVwith non-interacting Green’s functions.
SystemLabel_IVf.IA1BA: If
fullDOSis set toT, this file contains the total density of states computed at biasIVwith 1BA Green’s functions.
SystemLabel_IVf.IASCBA: If
fullDOSis set toT, this file contains the total density of states computed at biasIVwith SCBA Green’s functions.
In case of spin polarized calculation the *IVf.IA* files contain three columns, where the first corresponds to the energy (subtracted by the Fermi energy) and the second and third columns corresponds to the DOS for up and down spins, respectively.
In case of non-polarized spin calculation these files contain only a second column containing the DOS.
If fullDOS is set to T, the following files contain the projected density of states computed at bias IV:
SystemLabel_IVp.IA0: If
fullDOSis set toT, this file contains the projected density of states computed at biasIVwith non-interacting Green’s functions.
SystemLabel_IVp.IA1BA: If
fullDOSis set toT, this file contains the projected density of states computed at biasIVwith 1BA Green’s functions.
SystemLabel_IVp.IASCBA: If
fullDOSis set toT, this file contains the projected density of states computed at biasIVwith SCBA Green’s functions.
The *IVp.IA* files are structured using spacing and xml tags, and can be processed by the program in Util/pdosxml.
Molecular dynamics with transport
In the I-SMEAGOL code one can perform molecular dynamics (MD) and structural optimizations, as implemented in SIESTA, in non-equilibrium situation together with transport calculations. I-SMEAGOL has an outer bias loop, where the applied bias is changed according to the number of bias points set by the user, and an inner geometry loop, where the electronic structure, forces and stress are computed for a given geometry. Subsequently the atomic positions are updated according to the MD or optimization option (refer to the SIESTA manual to check the implemented options for MD and structural optimizations).
For all different MD options allowed by SIESTA, the key point are the forces and stress computations, which in most cases determines the next geometry step. Therefore, in the same way that we need to correct the density matrix in usual transport calculations, in order to include the effects of the applied bias and the leads coupling on MD, one should also correct the energy density, which is used for calculating the forces. The implementation of the non-equilibrium forces follows the methodology described in [7].
Input files
There are no additional input files besides those used for the I-V calculation (see above).
Input flags
The following input flags must be supplied to the file input.fdf in order to perform MD together with transport (I-V) calculations.
CalculateForces (Boolean): If true I-SMEAGOL will calculate the non-equilibrium energy density. Since this specification increases the time of the calculation, it should be used only when the force calculation is relevant (e.g. in MD and structural optimizations) and should be unset in ordinary transport calculations.
Default value:
F
SaveMDSteps (data block): Block containing information for printing the Hartree potential (
IV_MD.SystemLabel.VH), the charge density (IV_MD.SystemLabel.RHO), the converged density matrix (IV_MD.SystemLabel.DMT), the difference between the self-consistent and the atomic charge densities (IV_MD.SystemLabel.DRHO) and the total DFT potential (IV_MD.SystemLabel.VT) at a specified bias step and MD step. The bias steps are those specified atSaveBiasStepsblock (see SMEAGOL User’s Guide [6]). The arguments inSaveMDStepsblock are integers indicating the MD steps in which these information should be printed. Their values must be consistent with the chosenMD.TypeOfRun(refer to the SIESTA manual for the possible options). The appropriate SIESTA flag for printing any of these files must also be set to true.Example:
%block SaveBiasSteps 0 %endblock SaveBiasSteps %block SaveMDSteps 1 4 %endblock SaveMDStepsThen, for instance if the SIESTA flag
SaveElectrostaticPotentialis set to true, I-SMEAGOL will print the files0_1.SystemLabel.VHand0_4.SystemLabel.VHcorresponding to the Hartree potential calculated at bias 0 and MD steps 1 and 4, respectively.Default value: No Default
Output files
The output files are the same as those obtained in I-V calculations, the only difference corresponds to the files prefixed by the IV bias step specified in SaveBiasSteps.
In MD they are prefixed by the IV bias step specified in SaveBiasSteps and by the MD step specified in SaveMDSteps as: IV_MD.SystemLabel.
How to run I-SMEAGOL
Assuming that the user has already compiled I-SMEAGOL successfully and saved it as an executable (say i-smeagol.2.0), then we are ready to start a calculation.
Initially the user must setup the input file for the left- and right-hand side leads.
The input file must include the appropriate SIESTA and I-SMEAGOL flags as discussed in above and in the SIESTA and SMEAGOl manuals.
Let us assume, as a simple example, that the two leads are equivalent and the leads file is called leads.fdf.
In the same directory where this file is, there must also be the pseudopotential files - either in .psf or .vps format.
Then the user should type:
i-smeagol.2.0 < leads.fdf > leads.out
The calculation will yield the files bulklft.DAT, bulkrgt.DAT, SystemLabel.HSL and SystemLabel.DM.
These should be moved to the directory containing the input file for the scattering region - say scattering.fdf.
This directory must also contain pseudopotential files for all the atomic species involved in the calculation.
It is important to note that the user must be consistent with regards to pseudopotentials, they should be identical to the ones used for the leads calculation.
Before starting the I-V calculation we must obtain HartreeLeadsBottom.
For that we use the post-processing tool Pot.exe contained in the Utils directory of the SMEAGOL distribution.
The file Potential.dat should be edited in order to process the file SystemLabel.VH (for the leads).
The resulting output SystemLabel-VH_AV.dat can be viewed using a plotting tool of preference.
We are interested in the first two columns of this data file.
They contain the planar average of the Hartree potential as a function of the z direction.
A value for the Hartree potential (HartreeLeadsBottom) should be chosen (usually the edges of the unit cell) and the position in the unit cell should be recorded and matched with the equivalent position in the scattering region (HartreeLeadsLeft and HartreeLeadsRight).
In case of periodic lead calculation, another bulk calculation should be performed considering only the lead’s unit cell:
i-smeagol.2.0 < leadSmall.fdf > leadSmall.out
The calculation will yield the files bulklft.DAT, bulkrgt.DAT, SystemLabelSmall.HSL and SystemLabelSmall.xij.
Since the files bulklft.DAT and bulkrgt.DAT have the same name as those from the previous bulk calculation, one should rename them as bulklftsmall.DAT and bulkrgtsmall.DAT, respectively.
After that all four files should be moved to the directory where the transport calculations will be performed.
Once this is done, we are ready to calculate the I-V characteristics:
i-smeagol.2.0 < scattering.fdf > scattering.out
The resulting files can be processed using a plotting programs of preference.
Problem Handling
The users are encouraged to report problems and bugs to the I-SMEAGOL’s developers at bitbucket. Patches and fixes will be uploaded to the web-site https://bitbucket.org/brandimarte/smeagol-2.0/wiki/Home.
Acknowledgements
PBM thanks CNPq (National Council of Technological and Scientific Development) for financial support (grant 142792/2010-1).
References
[4] http://departments.icmab.es/leem/siesta/
[5] H. Haug and A.-P. Jauho, Quantum Kinetics in Transport and Optics of Semiconductors, Springer, Berlin (1994).
[6] SMEAGOL User’s Guide comes along with the code at: http://www.smeagol.tcd.ie
[7] R. Zhang, I. Rungger, S. Sanvito and S. Hou, Phys. Rev. B 84, 085445 (2011).